Interesting fact: this figure is related to fractals.
 |
| Steps in the construction of the Koch curve |
Fractals are ubiquitous. Unbeknown to most students, such geometric objects can be applied in many disciplines, offering scientists and artists alike limitless exploration. In this post, I will introduce fractals to you.
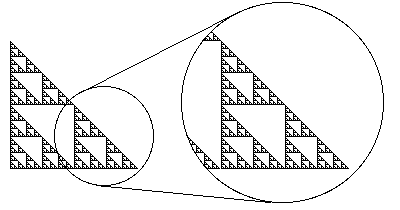 |
| Small pieces resemble the whole. |
A fractal is an image with an infinite amount of of self-similarity, meaning that if you keep zooming in on such an object, you will see the same shape repeated endlessly, as seen in the figure above.
Terminologies related to fractals:
Iterated function
Basic idea: Start with an input. Then take the output as the next input. Repeat this process several times.
Say we have a squaring function $f(x)=x^2$.
$3 \stackrel{f}{\rightarrow} 9 \stackrel{f}{\rightarrow} 81 \stackrel{f}{\rightarrow} 6561 \cdots$
initial condition/seed (denoted by $x_0$): the number we start with, 3 in this case
Iterating a function produces a sequence of numbers which is called an itinerary/orbit. (This is consistent with the everyday usage of the term; an itinerary is a list, in order, of all the places visited along a journey.)
Notation:
$x_1=f(x_0)$
$x_2=f(x_1)=f(f(x_0))$
$x_3=f(x_2)=f(f(f(x_0)))$
$\vdots$
$x_{11}=f(f(f(f(f(f(f(f(f(f(f(x_0)))))))))))$
A better notation would be:
$f(f(x))=f^{(2)}(x)$
$f(f(f(x)))=f^{(3)}(x)$
In general, for n applications of f:
$\stackrel{\text{n times}}{f(f(f(\cdots f(x))))}=f^{(n)}(x)$
Note: Don't mix it up with derivatives.
Why Iteration?
Affine Transformations
Fixed points
Julia sets
Dynamical systems
Vector Quantization
[later]
Applications:
Computer Science:
Computer graphics
- simulate photo-realistic landscapes and scenery used in films and video games
- model organic objects and textures such as clouds, trees, fog, and water
Image compression
- scale down size of images to reduce the savings in space (The Compression ratio is huge since the compressed file is represented by an iterated function that requires dramatically less storage.)
Economics:
- demonstrate how the activity of markets accelerates and decelerates: the essence of volatility
- analyze the trend of shares on the stock market based on multifractals
- predict the future behaviour of share prices by studying variations in the past
- elucidate sophisticated economics phenomena
Science:
- measure the variation between normal and diseased structures
- construct fractal antennas
Management:
- manage industrial supply chains and transport systems
Chaos Theory


No comments:
Post a Comment